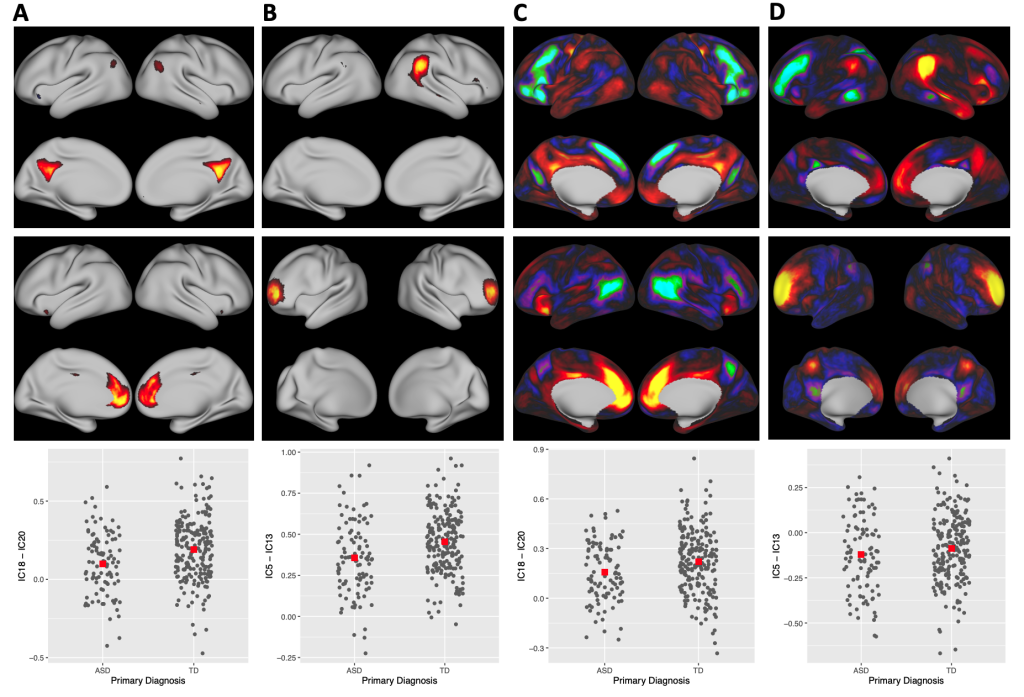
We develop and apply methods that reveal biological features from high-dimensional data. Independent component analysis (ICA) is a popular technique in the analysis of functional magnetic resonance imaging (fMRI), where it is used to estimate resting-state networks and artifacts. We developed Sparse ICA, which estimates the non-zero brain locations that work together in a resting-state network. Popular approaches use unpenalized ICA methods followed by thresholding. Our approach is fast, interpretable, and can be more accurate. We have developed practical tools and guidelines to help researchers improve the application of ICA to fMRI, with an emphasis on multiple initializations for non-convex optimization in high dimensional analyses. We developed a method for non-Gaussian component analysis that uses a likelihood as a measure of information to achieve dimension reduction. We developed Simultaneous Non-Gaussian Component Analysis (SING) to extract joint information across multiple neuroimaging datasets, for example, task and resting-state fMRI. Our approach extracts joint scores while maximizing the non-Gaussianity of the feature space. Our application revealed resting-state functional connectivity patterns linked with a working memory task. An R package implementing this method is available.